Programando un Perceptron en Python
Si estás acá, estás dando un importante primer paso en entender los múltiples algoritmos de machine learning. En este artículo revisaremos cómo funciona un perceptron e implementaremos un ejemplo en python usando el conocido dataset Iris.
El perceptron
El Perceptron simple, también conocido una red neuronal de una sola capa (Single-Layer Neural Network), es un algoritmo de clasificación binaria creado por Frank Rosenblatt a partir del modelo neuronal de Warren McCulloch y Walter Pitts desarrollado en 1943.
La idea tras la Neurona MCP y el Perceptron con umbral de Rosenblatt es usar un enfoque simple para simular el funcionamiento de una neurona en el cerebro.
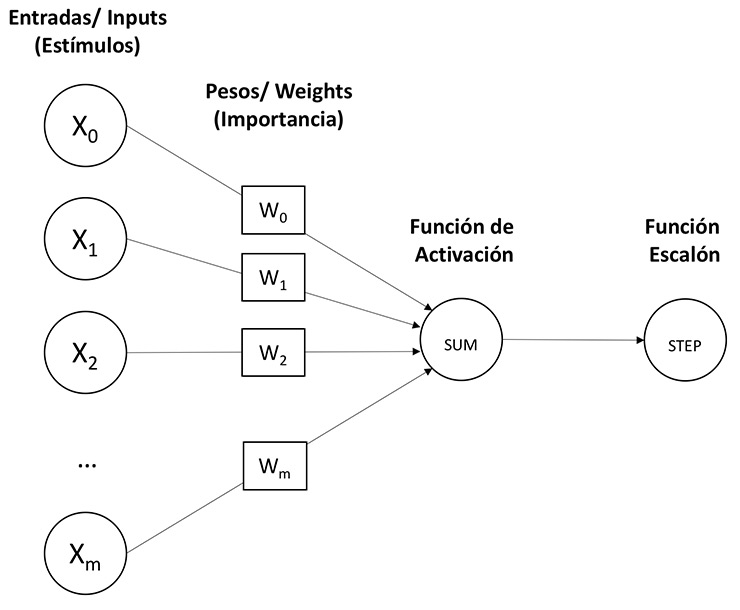
La neurona recibe impulsos externos (\(x\)) que son considerados con distinta importancia o peso (\(w\)) en una función de activación (\(z\)). Si el estímulo agregado sobrepasa cierto umbral (\(\theta\)), la neurona se activa.
Matemáticamente, definimos \(x\) como el vector de estímulos y \(w\) como el vector de pesos, ambos m dimensiones, y \(z\) como la función de activación.
\[
w =
\begin{bmatrix}
w_{1} \\ \vdots \\ w_{m}
\end{bmatrix},
x =
\begin{bmatrix}
x_{1} \\ \vdots \\ x_{m}
\end{bmatrix} \\
z = w^{T} \cdotp x \\
z = w_{1}x_{1} + \ldots + w_{m}x_{m}
\]
El perceptron \( \phi (z) \) se considera activo cuando su valor es mayor o igual al umbral \( \theta \) o inactivo en cualquier otro caso. Formalmente esta es una función escalón puede ser escrita de la siguiente forma:
\[
\phi (z) =
\left\{
\begin{array}{ll}
1 & si\; z\geq \theta \\
-1 & Cualquier\; otro\; caso \\
\end{array}
\right.
\]
Si incorporamos \(\theta\) a la expresión, definiendo \(w_{0} = -\theta \;y\; x_{0} = 1\) podemos escribir \(z = w_{0}x_{0} + w_{1}x_{1} + \ldots + w_{m}x_{m} \\\).
\[
\phi (z) =
\left\{
\begin{array}{ll}
1 & si\; z\geq 0\\
-1 & Cualquier\; otro\; caso \\
\end{array}
\right.
\]
La regla de aprendizaje
El perceptron tiene una regla de aprendizaje bastante simple que le permite ir ajustando los valores de los pesos (\(w\)). Para ello, se siguen los siguientes pasos:
- Asignar un valor inicial a los pesos de 0 (cero) o valores pequeños al azar.
- Para cada muestra de entrenamiento \(x^{(i)}\) hacer lo siguiente
- Computar el valor de salida \(\hat{y}\).
- Actualizar los pesos.
La actualización de los pesos se hace incrementando o disminuyéndolos en \(\Delta w_j\)
\[
w_{j} := w_{j} + \Delta w_{j}\\
\Delta w_{j} = \eta (y^{(i)} – \hat{y}^{(i)})x_{j}^{(i)}
\]
Donde:
- \(\eta\) es la tasa de aprendizaje que es un valor entre 0 y 1.0
- \(y^{(i)}\) es el valor real
- \(\hat{y}^{(i)}\) es el valor de salida calculado (notar el sombrero en la y)
- \(x_{j}^{(i)}\) es el valor de la muestra asociado
Esto implica que si el valor real y el valor calculado son el mismo, \(w\) no es actualizado o mejor dicho \(\Delta w_{j} = 0\) . Sin embargo, si hubo un error en la predicción el valor será actualizado en la diferencia entre el valor real y el predicho, ajustado por el valor de la muestra y la tasa de aprendizaje.
Nuestro ejemplo con el dataset Iris
Para este ejemplo usaremos un conjunto de datos llamado Iris que es quizás el dataset más conocido en el mundo del machine learning. Este es un dataset multivariado que contiene 50 muestras de 3 especies de la flor Iris (iris setosa, Iris virgínica e Iris versicolor). En cada caso, se midió en centímetros largo y ancho del sépalo y del pétalo. Pueden descargar los datos desde el Machine Learning Repository de la Universidad de California o desde mi repositorio en Github
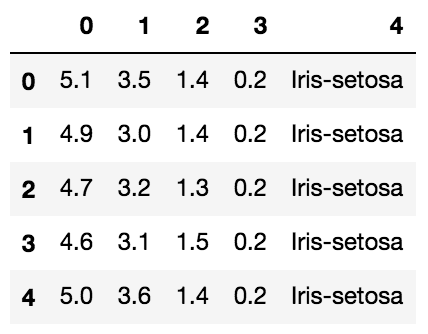
Los atributos disponibles en el dataset son los siguientes:
- Largo del sépalo en cm
- Ancho del sépalo en cm
- Largo del pétalo en cm
- Ancho del pétalo en cm
- Clase (Iris setosa, Iris versicolor, Iris virgínica)
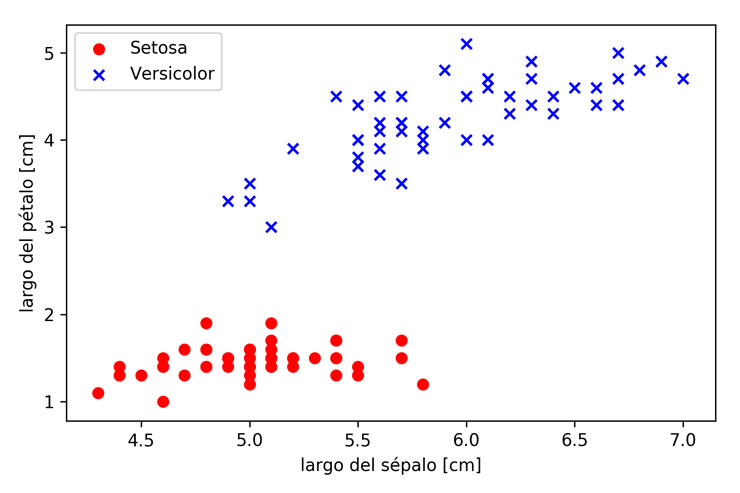
Una de las características de este dataset, es que algunos de sus atributos son linealmente separables, que es un requisito para el buen funcionamiento del perceptron. Que un set sea linealmente separable significa que una puede trazarse una recta (2D) o un plano (3D) y aislar cada clase de datos correctamente. Esto se puede observar claramente en el siguiente ejemplo.
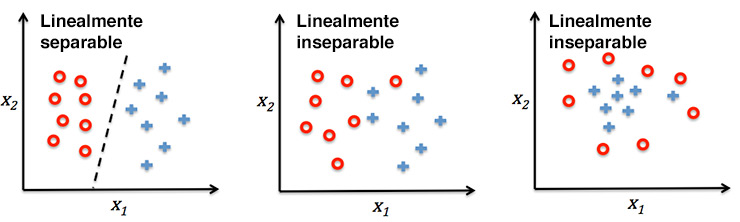
En el caso del dataset Iris, al graficar todas las clases por largo del pétalo y largo del sétalo, podemos ver que las setosas son linealmente separables de las virgínicas y las versicolor. No así las virgínicas de las versicolor.
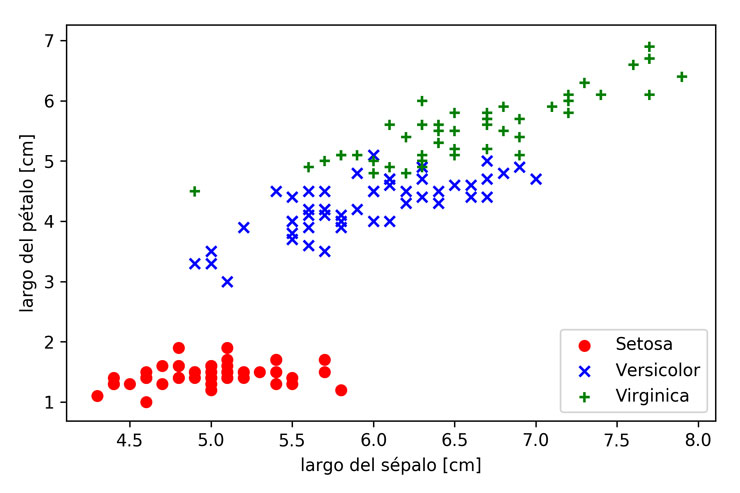
Por esta razón, en este artículo solo usaremos las clases Iris-setosa y Iris-versicolor para el clasificarlas con el perceptron.
Implementando la regla del perceptron en python
Puedes descargar el cuaderno de Jupyter desde el repositorio en Github y así ir siguiendo esta implementación paso a paso.
Primero partiremos implementando un clase en python. Esta clase define los siguientes métodos:
- __init__: Define la tasa de aprendizaje del algoritmo y el numero de pasadas a hacer por el set de datos.
- fit: Implementa la regla de aprendizaje, definiendo inicialmente los pesos en 0 y luego ajustándolos a medida que calcula/predice el valor para cada fila del dataset.
- predict: Es la función escalón \( \phi (z) \). Si el valor de z es mayor igual a 0,
tiene por valor 1. En cualquier otro caso su valor es -1. - net_input: Es la implementación de la función de activación z. Si se fijan en el código, hace producto punto en los vectores \(x\) y \(w\).
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 |
import numpy as np class Perceptron: """Clasificador Perceptron basado en la descripción del libro "Python Machine Learning" de Sebastian Raschka. Parametros ---------- eta: float Tasa de aprendizaje. n_iter: int Pasadas sobre el dataset. Atributos --------- w_: array-1d Pesos actualizados después del ajuste errors_: list Cantidad de errores de clasificación en cada pasada """ def __init__(self, eta=0.1, n_iter=10): self.eta = eta self.n_iter = n_iter def fit(self, X, y): """Ajustar datos de entrenamiento Parámetros ---------- X: array like, forma = [n_samples, n_features] Vectores de entrenamiento donde n_samples es el número de muestras y n_features es el número de carácteristicas de cada muestra. y: array-like, forma = [n_samples]. Valores de destino Returns ------- self: object """ self.w_ = np.zeros(1 + X.shape[1]) self.errors_ = [] for _ in range(self.n_iter): errors = 0 for xi, target in zip(X, y): update = self.eta * (target - self.predict(xi)) self.w_[1:] += update * xi self.w_[0] += update errors += int(update != 0.0) self.errors_.append(errors) return self def predict(self, X): """Devolver clase usando función escalón de Heaviside. phi(z) = 1 si z >= theta; -1 en otro caso """ phi = np.where(self.net_input(X) >= 0.0, 1, -1) return phi def net_input(self, X): """Calcular el valor z (net input)""" # z = w · x + theta z = np.dot(X, self.w_[1:]) + self.w_[0] return z |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
import pandas as pd import matplotlib.pyplot as plt # Cargamos el dataset df = pd.read_csv("../datasets/iris.data", header=None) # extraemos el largo sepal y el largo del pétalo en las columnas 0 y 2. Usaremos solo Setosa y Versicolor X = df.iloc[0:100, [0, 2]].values # Seleccionamos Setosa y Versicolor. y = df.iloc[0:100, 4].values y = np.where(y == 'Iris-setosa', -1, 1) # Inicializamos el perceptron ppn = Perceptron(eta=0.1, n_iter=10) # Lo entrenamos con los vectores X e y ppn.fit(X, y) # Graficamos el número de errores en cada iteración plt.plot(range(1, len(ppn.errors_) + 1), ppn.errors_, marker='o') plt.xlabel('Epochs') plt.ylabel('Número de actualizaciones') plt.tight_layout() plt.show() |
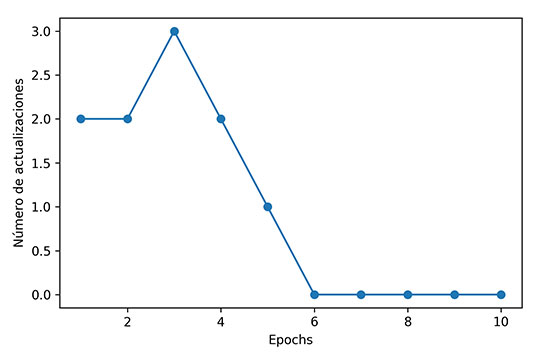
Una vez entrenado, pueden ver los valores del modelo imprimiendo las principales variables:
|
1 2 3 4 5 6 7 8 9 10 11 |
print("Theta: " + str(ppn.w_[0])) print("W: " + str(ppn.w_[1:])) print("X: [Largo sépalo, Largo pétalo]") print("z = W · X") print("phi(z) = 1 si z >= theta; -1 c.o.c") # Theta: -0.4 # W: [-0.68 1.82] # X: [Largo sépalo, Largo pétalo] # z = W · X # phi(z) = 1 si z >= theta; -1 c.o.c |
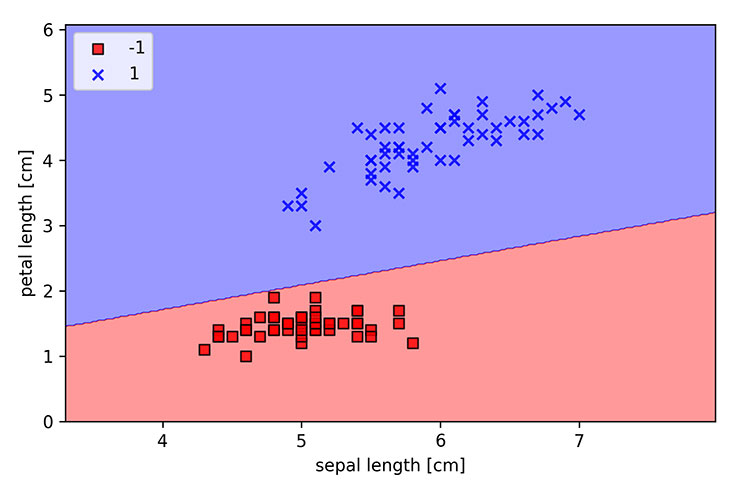
Y al graficar el modelo, podemos ver cómo las setosas quedan separadas por una recta de las versicolor.
Conclusión
El perceptron es un modelo simple, reduccionista y con muchas limitaciones, pero es un excelente ejemplo introductorio a los clasificadores y a las redes neuronales. A la primera leída, quizás no sea tan simple de entender, pero te recomiendo descargar el cuaderno jupyter desde el repositorio y revisarlo con calma.
| Si quieres profundizar te recomiendo revisar los siguientes libros que a mi me han ayudado bastante: |  |
 |
Este es el primero artículo/tutorial que escribo de machine learning. Les agradecería s me pudieran dejar cualquier recomendación para poder hacerlos más claros de entender. Si tienen cualquier duda, déjenla en los comentarios y haré lo posible por responderla.
¡Saludos!


muy util! gracias!!
muchas gracias, bastante completo y facil de entender
Se agradece. Que bueno haber podido ayudar.
Muy buena explicación!! Voy a bajar el cuaderno Jupiter para practicar
Excelente! Éxito.